The problem with Huffman coding in the above message is that it can’t create codes with the exact information content required. In most cases it is a little above or a little below, leading to deviations from the optimum. But arithmetic coding gets to within a fraction of a percent of the actual information content, resulting in more accurate coding.

Arithmetic coding requires more CPU power than was available until recently. Even now it will generally suffer from a significant speed disadvantage when compared to older coding methods. But the gains from switching to this method are significant enough to ensure that arithmetic coding will be the coding method of choice when the cost of storing or sending information is high enough.

Modeling

If we use a an automotive metaphor for data compression, coding would be the wheels, but modeling would be the engine. Regardless of the efficiency of the coder, if it doesn’t have a model feeding it good probabilities, it won’t compress data.

Lossless data compression is generally implemented using one of two different types of modeling: statistical or dictionary-based. Statistical modeling reads in and encodes a single symbol at a time using the probability of that character’s appearance. Dictionary-based modeling uses a single code to replace strings of symbols. In dictionary-based modeling, the coding problem is reduced in significance, leaving the model supremely important.

Statistical Modeling

The simplest forms of statistical modeling use a static table of probabilities. In the earliest days of information theory, the CPU cost of analyzing data and building a Huffman tree was considered significant, so it wasn’t frequently performed. Instead, representative blocks of data were analyzed once, giving a table of character-frequency counts. Huffman encoding/decoding trees were then built and stored. Compression programs had access to this static model and would compress data using it.

But using a universal static model has limitations. If an input stream doesn’t match well with the previously accumulated statistics, the compression ratio will be degraded—possibly to the point where the output stream becomes larger than the input stream. The next obvious enhancement is to build a statistics table for every unique input stream.

Building a static Huffman table for each file to be compressed has its advantages. The table is uniquely adapted to that particular file, so it should give better compression than a universal table. But there is additional overhead since the table (or the statistics used to build the table) has to be passed to the decoder ahead of the compressed code stream.

For an order-0 compression table, the actual statistics used to create the table may take up as little as 256 bytes—not a very large amount of overhead. But trying to achieve better compression through use of a higher order table will make the statistics that need to be passed to the decoder grow at an alarming rate. Just moving to an order 1 model can boost the statistics table from 256 to 65,536 bytes. Though compression ratios will undoubtedly improve when moving to order-1, the overhead of passing the statistics table will probably wipe out any gains.

For this reason, compression research in the last 10 years has concentrated on adaptive models. When using an adaptive model, data does not have to be scanned once before coding in order to generate statistics. Instead, the statistics are continually modified as new characters are read in and coded. The general flow of a program using an adaptive model looks something like that shown in Figures 2.2 and 2.3.

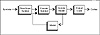
Figure 2.2  General Adaptive Compression.

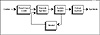
Figure 2.3  General Adaptive Decompression.

The important point in making this system work is that the box labeled “Update Model” has to work exactly the same way for both the compression and decompression programs. After each character (or group of characters) is read in, it is encoded or decoded. Only after the encoding or decoding is complete can the model be updated to take into account the most recent symbol or group of symbols.

One problem with adaptive models is that they start knowing essentially nothing about the data. So when the program first starts, it doesn’t do a very good job of compression. Most adaptive algorithms tend to adjust quickly to the data stream and will begin turning in respectable compression ratios after only a few thousand bytes. Likewise, it doesn’t take long for the compression-ratio curve to flatten out so that reading in more data doesn’t improve the compression ratio.

One advantage that adaptive models have over static models is the ability to adapt to local conditions. When compressing executable files, for example, the character of the input data may change drastically as the program file changes from binary program code to binary data. A well-written adaptive program will weight the most recent data higher than old data, so it will modify its statistics to better suit changed data.

Dictionary Schemes

Statistical models generally encode a single symbol at a time— reading it in, calculating a probability, then outputting a single code. A dictionary-based compression scheme uses a different concept. It reads in input data and looks for groups of symbols that appear in a dictionary. If a string match is found, a pointer or index into the dictionary can be output instead of the code for the symbol. The longer the match, the better the compression ratio.

This method of encoding changes the focus of dictionary compression. Simple coding methods are generally used, and the focus of the program is on the modeling. In LZW compression, for example, simple codes of uniform width are used for all substitutions.

A static dictionary is used like the list of references in an academic paper. Through the text of a paper, the author may simply substitute a number that points to a list of references instead of writing out the full title of a referenced work. The dictionary is static because it is built up and transmitted with the text of work—the reader does not have to build it on the fly. The first time I see a number in the text like this—[2]—I know it points to the static dictionary.

The problem with a static dictionary is identical to the problem the user of a statistical model faces: The dictionary needs to be transmitted along with the text, resulting in a certain amount of overhead added to the compressed text. An adaptive dictionary scheme helps avoid this problem.