| Previous | Table of Contents | Next |
Chapter 3
The Dawn Age: Minimum Redundancy Coding
In the late 1940s, the early years of Information Theory, the idea of developing efficient new coding techniques was just starting to be fleshed out. Researchers were exploring the ideas of entropy, information content, and redundancy. One popular notion held that if the probability of symbols in a message were known, there ought to be a way to code the symbols so that the message would take up less space.
Remarkably, this early work in data compression was being done before the advent of the modern digital computer. Today it seems natural that information theory goes hand in hand with computer programming, but just after World War II, for all practical purposes, there were no digital computers. So the idea of developing algorithms using base 2 arithmetic for coding symbols was really a great leap forward.
The first well-known method for effectively coding symbols is now known as Shannon-Fano coding. Claude Shannon at Bell Labs and R.M. Fano at MIT developed this method nearly simultaneously. It depended on simply knowing the probability of each symbol’s appearance in a message. Given the probabilities, a table of codes could be constructed that has several important properties:
- • Different codes have different numbers of bits.
- • Codes for symbols with low probabilities have more bits, and codes for symbols with high probabilities have fewer bits.
- • Though the codes are of different bit lengths, they can be uniquely decoded.
- • Codes for symbols with low probabilities have more bits, and codes for symbols with high probabilities have fewer bits.
The first two properties go hand in hand. Developing codes that vary in length according to the probability of the symbol they are encoding makes data compression possible. And arranging the codes as a binary tree solves the problem of decoding these variable-length codes.
An example of the type of decoding tree used in Shannon-Fano coding is shown below. Decoding an incoming code consists of starting at the root, then turning left or right at each node after reading an incoming bit from the data stream. Eventually a leaf of the tree is reached, and the appropriate symbol is decoded.
Figure 3.1 is a Shannon-Fano tree designed to encode or decode a simple five-symbol alphabet consisting of the letters A through E. Walking through the tree yields the code table:
| Symbol | Code |
|---|---|
| A | 00 |
| B | 01 |
| C | 10 |
| D | 110 |
| E | 111 |
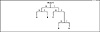
Figure 3.1 A simple Shannon-Fano tree.
The tree structure shows how codes are uniquely defined though they have different numbers of bits. The tree structure seems designed for computer implementations, but it is also well suited for machines made of relays and switches, like the teletype machines of the 1950s.
While the table shows one of the three properties discussed earlier, that of having variable numbers of bits, more information is needed to talk about the other two properties. After all, code trees look interesting, but do they actually perform a valuable service?
The Shannon-Fano Algorithm
A Shannon-Fano tree is built according to a specification designed to define an effective code table. The actual algorithm is simple:
- 1. For a given list of symbols, develop a corresponding list of probabilities or frequency counts so that each symbol’s relative frequency of occurrence is known.
- 2. Sort the lists of symbols according to frequency, with the most frequently occuring symbols at the top and the least common at the bottom.
- 3. Divide the list into two parts, with the total frequency counts of the upper half being as close to the total of the bottom half as possible.
- 4. The upper half of the list is assigned the binary digit 0, and the lower half is assigned the digit 1. This means that the codes for the symbols in the first half will all start with 0, and the codes in the second half will all start with 1.
- 5. Recursively apply the steps 3 and 4 to each of the two halves, subdividing groups and adding bits to the codes until each symbol has become a corresponding code leaf on the tree.
- 2. Sort the lists of symbols according to frequency, with the most frequently occuring symbols at the top and the least common at the bottom.
| Previous | Table of Contents | Next |