The Compress Main Program

The code for the compression program is short:

InitializeTree( &Tree );
while ( ( c = getc( input ) ) != EOF ) {
  EncodeSymbol( &Tree, c, output );
  UpdateModel( &Tree, c );
}
EncodeSymbol(  &Tree, END_OF_STREAM, output );

Once the tree has been initialized, the program sits in a loop encoding characters and updating the model. When there are no more characters left to encode, it encodes the end-of-stream symbol, and it is done.

Complexities are hidden in these functions. The EncodeSymbol function needs to see if the symbol is already defined. If it isn’t, EncodeSymbol needs to output the escape code and the unencoded symbol. EncodeSymbol then needs to add the symbol to the tree, with a count of 0.

The UpdateModel function also hides some complexity. It performs the update discussed previously in the chapter, which is fairly complex. Before doing the update, it checks to see if the root node has reached the maximum allowable weight. If it has, the tree is scaled by a factor of two and rebuilt.

The Expand Main Program

Like the compress main program, the expand program is short and to the point. After initializing the tree, it reads in symbols via the DecodeSymbol routine, then writes them to the output file. After each symbol is decoded, it is written to the output file, and the model is updated.

As in the compress program, a certain amount of complexity is concealed in the higher-level functions. The DecodeSymbol routine has to see if the symbol it decodes is an escape code. If it is, DecodeSymbol throws away the escape code and reads in an “unencoded” 8-bit symbol. The symbol is then added to the Huffman tree, with an initial count of 0.

As previously seen, the UpdateModel() routine has to see if the root node has reached the maximum allowable count. If it has, the Huffman tree is rebuilt. After that, the normal increment/test/swap routine ensues.

InitializeTree( &Tree );
while ( ( c = DecodeSymbol( &Tree, input ) ) !=END_OF_STREAM ) {
  if ( putc( c, output ) == EOF )
    fatal_error( "Error writing character" );
  UpdateModel( &Tree, c );
}

Encoding the Symbol

After initializing the tree, the compress routine repeatedly calls the EncodeSymbol routine. The EncodeSymbol routine (shown below) first identifies the leaf node for the symbol to be encoded. If the leaf table returns a-1, it means that this symbol is not presently found in the Huffman tree. In that case, the symbol to be encoded is switched to the escape code, and its root node is located.

The encoding process for a Huffman tree works by starting at the leaf node and moving up through the parent nodes one at a time, until the root is reached. In a conventional Huffman tree, there will usually be two child nodes for each parent, one that encodes a 0 bit and another that encodes a 1 bit. The data structures used in this program take advantage of the sibling property by always grouping the two children of a parent node next to one another in the node list.

Grouping children together saves space by requiring only a single child pointer instead of two. It also means that a child automatically knows whether it is the child that encodes a 1 or 0 by whether it is odd or even. In this program, the odd child is arbitrarily designated the 1, and the even is always the 0.

Given this information, the encoding process is accomplished without too many lines of C code. Starting at the leaf node, each bit is added to the cumulative Huffman code. Whether the bit is a 1 or a 0 determines whether the bit is odd or even. As each bit is encoded, the current_bit mask is shifted by one so the next bit encoded will appear in the next most significant position. A counter is also incremented that keeps track of how many bits have been accumulated in the output word so far.

code = 0;
current_bit = 1;
code_size = 0;
current_node = tree->leaf[ c ];
if ( current_node == -1 )
    current_node = tree->leaf[ ESCAPE ];
while ( current_node != ROOT_NODE  ) {
    if ( ( current_node & 1 ) == 0 )
       code | = current_bit;
    current_bit <<= 1;
    code_size++;
    current_node = tree->nodes[ current_node ].parent;
};
OutputBits( output, code, code_size );
if ( tree->leaf[ c ] == -1 ) {
    OutputBits( output, c, 8 );
    add_new_node( tree, c );
}

After the bits of the Huffman code have been accumulated in the code word, the utility routine OutputBits (found in BITIO.C) is called to send out the code. There is still one piece of work left to do, however, before returning. If the code that was just output was the escape code, we have to handle the special condition created when a previously unreferenced symbol is encountered.

The first step taken after the escape code is sent is simple. The new symbol is output in an unencoded fashion, just as it was read in from the file. This lets the decoder know what symbol to add to the table. The second step is to add the new node to the Huffman tree. When the new node is added to the tree, it is inserted with a weight of 0. The 0-weight node will be incremented later when the model is updated, so it will not be 0 for long. The advantage to adding a node with a weight of zero is that it can be done without having to worry about updating any other nodes or, worse, changing the shape of the tree.

Using the sibling property definitions, we know that if the new node has a weight of 0, it will be the very first node in the list, since nodes are ranked in order of weight. We add the node to the table by finding the presently lowest-weight node and break it out into two new nodes. The old lowest-weight node will be one of the two new nodes, and the new 0-weight node will be the other one.

Figure 4.10 illustrates how this process modifies a working tree. The Huffman tree has already had the A, B, C, and D nodes defined with nonzero weights. The A node has the lowest count and consequently is at the start of the list (remember that the list in this program has the highest weights at 0). When symbol E is going to be added to the tree, we first identify A as the node at the end of the list. The position A used to occupy is converted to an internal node, and two new nodes are created. Since E is guaranteed to have the lowest weight in the tree, it is set to be the first node in the list, and A is set to be the second node.

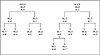
Figure 4.10  The Huffman tree before and after addition of a zero weight node.