The loop that creates internal nodes starts with j pointing to the next node that needs to be defined; i is an index that points to the next pair of nodes to be combined into an internal node. The loop progressively steps through the nodes, combining and adding new internal nodes until reaching the root node at location 0.

The process of creating the new internal node is simple. The new node, located at index j, is assigned a weight. The weight is simply the sum of the two nodes at location i, as would be expected. The hard work comes next. After node j is created, we have to decide where it belongs in the node list. The decision on where the new node belongs is made based on the weights of the nodes in the list. Recall that the sibling property says that the nodes have to be listed based on increasing weight. We have to step through the list till we find the first node that is less that the new node j, then place the new node immediately adjacent to that node in the list. Here is the procedure for the correct location for j:

for ( i = tree->next_free_node - 2 ; j >= ROOT_NODE ;
     i -= 2, j–– ) {
   k = i + 1;
   tree->nodes[ j ].weight = tree->nodes[ i ].weight +
                              tree->nodes[ k ].weight;
   weight = tree->nodes[ j ].weight;
   tree->nodes[ j ].child_is_leaf = FALSE;
       for ( k = j + 1 ; weight < tree->nodes[ k ].weight ; k++)
          ;
   k––;
  memmove( &tree->nodes[ j ]. &tree->nodes[ j + 1 ],
             ( k - j ) * sizeof( struct node ) );
   tree->nodes[ k ].weight = weight;
   tree->nodes[ k ].child = i;
   tree->nodes[ k ].child_is_leaf = FALSE;
}

The variable ‘weight’ is assigned the weight of the new internal node. The routine then loops back through the list until it finds the first node with a weight less than or equal to the weight of j. Node j will be placed immediately after that node in the list. Before that node can be positioned, we need to make room in the list by moving all the nodes that have higher weights up by one position. This is done with the memmove() function. After that, the new node has its child and weight assigned, and the loop continues.

This process can be seen in the short list of nodes about to be rebuilt in Figure 4.11. After having been rescaled, symbols A, B, C, and D have weights of 1, 3, 5, and 7 respectively. After the internal nodes have been stripped out, the list of nodes looks like Figure 4.11.

Figure 4.11  The list of nodes after the internal nodes have been stripped.

The first two nodes to be combined will be B and A, creating a new node, j, at location 2 in the table. By stepping back through the list from location 2, we see that the resulting internal node belongs between locations 4 and 5, right before B. After the memory move function is executed and the node is connected, the partial Huffman tree looks like this:

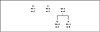
Figure 4.12  A partial Huffman tree after the memory move function is executed.

Because we are moving nodes around so freely, we do not assign parent pointers during this process. Once a node has been assigned as a child to another node, it is not going to change position in the list. But parent nodes that have yet to be combined together as children of another internal node may be moved farther up in the list as other nodes are combined. If we assigned parent nodes earlier in the process, every time we moved a node we would have to go through a backtracking procedure to locate its children and update their parent indices. We bypass this costly procedure by deferring parent node building to the third and final step in the Rebuild procedure. Assigning parent nodes is fairly simple. We start at the root node, and locate the children of each node in the tree. The children then have their parent node index set. If the child is a leaf instead of another node, the leaf[] array node index is set.

for ( i = tree->next_free_node - 1 ; i >= ROOT_NODE ; i-- ) {
  if ( tree->nodes[ i ].child_is_leaf ) {
    k = tree->nodes[ i ].child;
    tree->leaf[ k ] = i;
  } else {
    k = tree->nodes[ i ].child;
    tree->nodes[ k ].parent = tree->nodes[ k + 1 ].parent = i;
  }
}

Decoding the Symbol

The final high-level procedure to be discussed here is the routine used to decode an incoming symbol. Like the symbol encoder, this routine is short and simple. It starts at the root node of the tree and reads in a single bit at a time. As each bit is read in, one of the two children of the node is selected based on whether the input bit is a one or a zero. Eventually, this leads the routine to a leaf node.

When the leaf node is reached, we have decoded a symbol. The only possible complication at this point is if the decoded symbol is an escape code. If so, the symbol encoded by the encoder did not yet appear in the Huffman tree. This means that the next eight bits in the stream will contain an unencoded version of the symbol. If this is the case, the input routine is called to get the plain-text version of the symbol.

current_node = ROOT_NODE;
while ( !tree->nodes[ current_node ].child_is_leaf ) {
  current_node = tree->nodes[ current_node ].child;
  current_node += InputBit( input );
}
c = tree->nodes[ current_node ].child;
if ( c == ESCAPE ) {
  c = (int) InputBits( input, 8 );
  add_new_node( tree, c );
}
return( c );

Either the decoded symbol or the escaped plain version of the symbol is passed back to the calling program where it can be placed in the output file. The hard work will come after the symbol is decoded, when the tree has to be updated to reflect the newly arrived symbol.