| Previous | Table of Contents | Next |
DeleteString()
DeleteString() is called from the main compression loop every time a new character is read into the look-ahead buffer. It uses a standard binary tree deletion algorithm to delete a phrase from the text window.
DeleteString() first determines whether the node is really in the tree. It is possible for the AddString() routine to have already deleted a string because it was a duplicate. If this is the case, the work has been done, and the routine can return.
void DeleteString( int p )
{
int replacement;
if ( tree[ p ].parent == UNUSED )
return;
if ( tree[ p ].larger_child == UNUSED )
ContractNode( p. tree[ p ].smaller_child );
else if ( tree[ p ].smaller_child == UNUSED)
ContractNode( p, tree[ p ].larger_child );
else {
replacement = FindNextNode( p );
DeleteString( replacement );
ReplaceNode( p, replacement );
}
}
If the string is presently in the tree, there are two possibilities for a deletion strategy. If either of the node’s children are unused, deleting the node is just a matter of closing the link between the current node’s parent and the child in use, effectively pulling the node out of the tree. This is done by a routine called ContractNode().
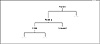
Figure 8.9 Tree before contraction of node p.
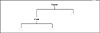
Figure 8.10 Tree after contraction of node p.
The situation is a little more complicated if the node to be deleted has children on both the larger_child and smaller_child nodes. When this is the case, the alternate deletion algorithm has to be used. The way to delete node p when both children are used to find the node in the tree either directly before or indirectly after node p in the ordered list of nodes. In this program, we find the next smaller node. This is done in the FindNextNode() routine and is accomplished by taking the first smaller_child branch, then following the larger_child branches until an UNUSED smaller_child is found. This next smaller node in the list is the replacement node.
The replacement node is then deleted from the tree, with a recursive call to DeleteString(). Out of control recursion is not a worry at this point, since the replacement node by definition has at least one UNUSED child. This means we will never go more than one level deep in our recursion.
After the replacement node has been deleted, it is used to replace the original deleted node. This is done by a routine called ReplaceNode() which simply inserts it in the tree in the same position as the original node.
Binary Tree Support Routines
The support routines used by AddString() and DeleteString() are ContractNode(), ReplaceNode(), and FindNextNode(). ContractNode() deletes a node when one of the children is UNUSED. To do this, the used child is linked with the parent, effectively pulling the node out of the tree. The deleted node has its parent node set to UNUSED, which is what is used internally to determine if a node is in use.
void ContractNode( int old_node, int new_node )
{
tree[ new_node ].parent = tree[ old_node ].parent;
if ( tree[ tree[ old_node ].parent ].larger_child == old_node )
tree[ tree[ old_node ].parent ].larger_child = new_node;
else
tree[ tree[ old_node ].parent ].smaller_child = new_node;
tree[ old_node ].parent = UNUSED;
}
ReplaceNode() is used during the deletion process when a new_node is going to be dropped into the tree on top of the old_node. It is assumed that the new_node is not currently linked to the tree. When the operation completes, the old_node will have been removed, and this is indicated by setting the parent to UNUSED.
void ReplaceNode( int old_node, int new_node )
{
int parent;
parent = tree[ old_node ].parent;
if ( tree[ parent ].smaller_child == old_node )
tree[ parent ].smaller_child = new_node;
else
tree[ parent ].larger_child = new_node;
tree[ new_node ] = tree[ old_node ];
tree[ tree[ new_node ].smaller_child ].parent = new_node;
tree[ tree[ new_node ].larger_child ].parent = new_node;
tree[ old_node ].parent = UNUSED;
}
FindNextNode() is called when the DeleteString() routine needs to find the next smaller node in the sorted list. It first takes the smaller branch from the starting node, then follows the larger branches until an UNUSED child is located. The node with the UNUSED larger_child is the next highest in the list. This routine assumes that the node has a next smallest node, meaning it has to have a smaller_child branch.
int FindNextNode( int node )
{
int next;
next = tree[ node ].smaller_child;
while ( tree[ next ].larger_child != UNUSED )
next = tree[ next ].larger_child;
return( next );
}
| Previous | Table of Contents | Next |