| Previous | Table of Contents | Next |
LZ78 Details
When using the LZ78 algorithm, both encoder and the decoder start off with a nearly empty dictionary. By definition, the dictionary has a single encoded string—the null string. As each character is read in, it is added to the current string. As long as the current string matches some phrase in the dictionary, this process continues.
But eventually the string will no longer have a corresponding phrase in the dictionary. This is when LZ78 outputs a token and a character. Remember that the string did have a match in the dictionary until the last character was read in. The current string, therefore, is defined as that last match with one new character added on. This is what LZ77 outputs: the index for the previous match and the character that broke that match.
But at this point, LZ78 takes an additional step. The new phrase, consisting of the dictionary match and the new character; is added to the dictionary. The next time that phrase appears, it can be used to build an even longer phrase.
A code fragment to implement this algorithm is shown next. Some of the detail has been glossed over, but this is a fairly faithful representation of the algorithm.
for ( ; ; ) {
current_match = 1;
current_length = 0;
memset( test_string, '\0', MAX_STRING );
for ( ; ; ) {
test_string[ current_length++ ] = getc( input );
new_match = find_match( test_string );
if ( new_match == -1 )
break;
current_match = new_match;
}
output_code( current_match );
output_char( test_string[ current_length - 1 ] );
add_string_to_dictionary( test_string );
}
By definition, the empty string will always match string 0, the null node in the dictionary. Thus, when we encounter a character for the first time, it is encoded as phrase 0 plus the new character. The next time that character appears, it will be encoded as part of a phrase.
An example of the encoder output follows. The input text is a sequence of words from the dictionary of a spelling checker. The LZ78 encoder starts encoding with no phrases in the dictionary; therefore, the first character it reads in from the input text, ‘D’, creates a string that has no match in the dictionary. The encoders will then output a phrase/character pair, in this case 0 and ‘D’. Remember that the dictionary starts up with zero defined as the empty phrase.
Input text: "DAD DADA DADDY DADO..."
| Output Phrase | Output Character | Encoded String |
|---|---|---|
| 0 | ‘D’ | “D” |
| 0 | ‘A’ | “A” |
| 1 | ‘ ‘ | “D “ |
| 1 | ‘A’ | “DA” |
| 4 | ‘ ‘ | “DA “ |
| 4 | ‘D’ | “DAD” |
| 1 | ‘Y’ | “DY” |
| 0 | ‘ ‘ | “ “ |
| 6 | ‘O’ | “DADO” |
The first two characters to come through the encoder, ‘D’ and ‘A,’ have not been seen before. Each will have to be encoded as a phrase, 0+ character pair. “D” is added to the dictionary as phrase 1, and “A” is added as phrase 2.
When the third character, ‘D,’ is read in, it matches an existing dictionary phrase. The ‘ ’ character, the next character read in, creates a new phrase with no match in the dictionary. LZ78 will output code 1 for the previous match (the D string), then the “ ” character.
As the encoding continues, the dictionary quickly builds up fairly long phrases. Of course, since these entries are from a dictionary sorted in alphabetical order, we probably build up phrases much faster than would normally be the case. After just nineteen characters have been read in and encoded, the dictionary looks like the one following.
| 0 | “” |
| 1 | “D” |
| 2 | “A” |
| 3 | “D” |
| 4 | “DA” |
| 5 | “DA” |
| 6 | “DAD” |
| 7 | “DY” |
| 8 | “” |
| 9 | “DADO” |
LZ78 Implementation
Like LZ77, LZ78 can arbitrarily set the size of the phrase dictionary. And like LZ77, in LZ78 we have to worry about the effects of this in two ways. First, we have to consider the number of bits allocated in the output token for the phrase code. Second, and more importantly, we have to consider how much CPU time managing the dictionary will take.
In theory, LZ78 should compress better and better as the size of the dictionary increases. But this only holds true as the length of the input text tends towards infinity. In practice, smaller files will quickly begin to suffer as the code size grows larger.
The real difficulty with LZ78 actually comes in managing the dictionary. If we use a sixteen-bit code for the phrase index, for example, we can accommodate 65,536 phrases, including the null code. The phrases can vary tremendously in length, including the improbable possibility of 65,536 different versions of a phrase composed of runs of a single, repeated character.
These phrases are conventionally stored in a multiway tree. The tree starts at a root node, 0, the null string. Each possible character that can be added to the null string is a new branch of the tree, with each phrase created that way getting a new node number.
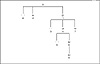
Figure 9.1 An LZ78 Dictionary Tree.
The dictionary tree shown here would be created after the previous nineteen-character phrase was encoded. The major difficulty with managing a tree such as this is the potentially large number of branches off of each node. When compressing binary files with an eight-bit alphabet, 256 branches off of each node are possible. We could simply allocate an array of indices or pointers at each node that was large enough to accommodate all 256 possible descendants. But since most nodes will not have that many descendants, it would be incredibly wasteful to allocate so much storage. Instead, descendant nodes are usually managed as a list of indices no longer than the number of descendant nodes that actually exits. This technique makes better use of available memory, but it is also significantly slower. It is essentially the same technique used in chapter 6 to perform higher-order modeling of data streams.
| Previous | Table of Contents | Next |