| Previous | Table of Contents | Next |
Problems and Results
How much can we compress voice files using conventional lossless techniques? To answer this question, a set of six short sound files were created, ranging in length from about one second to about seven seconds. To determine how compressible these files were, they were packed into an archive using ARJ 2.10, a shareware compression program that generally compresses as well or better than any other general-purpose program.
ARJ results showed that voice files did in fact compress relatively well. The six sample raw sound files gave the following results:
| Filename | Original | Compressed | Ratio |
|---|---|---|---|
| SAMPLE-1.RAW | 50777 | 33036 | 35% |
| SAMPLE-2.RAW | 12033 | 8796 | 27% |
| SAMPLE-3.RAW | 73091 | 59527 | 19% |
| SAMPLE-4.RAW | 23702 | 9418 | 60% |
| SAMPLE-5.RAW | 27411 | 19037 | 30% |
| SAMPLE-6.RAW | 15913 | 12771 | 20% |
These compression results look relatively promising. All the files were compressible to some extent, and some were reduced to less than half their original size. This level of compression is undoubtedly useful and may well be enough for some applications.
ARJ.EXE performs two sorts of compression on an input data stream. First, it does an LZSS type of windowed string matching on the string. The output from LZSS is, of course, a stream of tokens referring to either individual characters or matched strings. ARJ, like LHArc, takes LZSS a step further by performing Huffman compression on the output stream. Compressing these sound files using just LZSS compression and simple order-0 Huffman coding might tell us a little bit about what kind of redundancy is in these voice files.
To check the results, the files were compressed again with the LZSS program from Chapter 8 and the HUFF program from chapter 3. The results of these experiments are shown in the following table.
| Filename | ARJ Ratio | LZSS Ratio | HUFF Ratio |
|---|---|---|---|
| SAMPLE-1.RAW | 35% | 23% | 26% |
| SAMPLE-2.RAW | 27% | 5% | 30% |
| SAMPLE-3.RAW | 19% | 3% | 17% |
| SAMPLE-4.RAW | 60% | 25% | 27% |
| SAMPLE-5.RAW | 30% | 15% | 32% |
| SAMPLE-6.RAW | 20% | 2% | 18% |
The table shows that in every case, we perform more compression with simple order-0 Huffman coding than we do LZSS dictionary compression. Since LZSS is normally a much more powerful compression technique, this is a telling result.
What LZSS takes advantage of when compressing is repeated strings of characters in the file. Order-0 Huffman coding just takes advantage of overall frequency differences for individual sequences. What we see in these sounds files is some overall frequency difference between the various codes that make up the files, but not as many repeated strings as we might normally expect.
A look at snapshots of these sound files reveals some of the character of the data we are trying to compress. Figure 10.9 shows a section of about 600 sample points from SAMPLE-3.RAW. In this case, the sound samples are only taking up about 30 percent of the possible range allocated for them by the hardware. While individual samples can range from +127 to -128, in this snapshot they run only from about +30 to -30.
By only using a portion of the available bandwidth, a sound file automatically makes itself a good candidate for Huffman compression. The sample shown in Figure 10.9 can probably be compressed by about 30 percent by just squeezing the samples down from eight bits to six or so bits. This is, in effect, what the Huffman coder does.
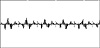
Figure 10.9 Sample points from SAMPLE-3.RAW.
Looking for repeated sequences in a sample such as this is less fruitful. We can certainly see a pattern in the waveform, but it is somewhat irregular, and it is not likely to produce many repeated patterns of even length 2. If we keep sampling long enough, random chance dictates that repeated strings will recur, but the compression will be much less than in a data or program file.
Figure 10.10 shows a sound sample that is a much more difficult candidate for compression. Unlike Figure 10.9, this sound sample utilizes nearly the entire dynamic range of the ADC, so an order-0 Huffman encoder will be much less effective. Likewise, the chances of finding repeated patterns with an LZSS algorithm diminish considerably here. This is the type of file that gives us only a few percentage points of compression.
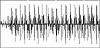
Figure 10.10 A sound sample that is difficult to compress.
Of course, even when looking at a “busy” sample like this, the human eye picks out patterns. The peaks and valleys of the waveform occur at somewhat regular intervals, telling us that sinusoidal waveforms are present in the signal. Unfortunately, our existing compression algorithms aren’t equipped to find this type of redundancy in an input waveform. To do better, we need to move to a new frontier: lossy compression.
Lossy Compression
The very word “lossy” implies that when using this type of compression we are going to give up a certain amount of precision. This would certainly not be acceptable when compressing the data or text files we use on our computers. We could probably compress the M&T Books annual financial statement if we rounded all figures off to the nearest million dollars, for example, but the accounting department would definitely have a problem working with the books after that.
By digitizing sound samples, however, we have in effect given up quite a bit of precision. For example, our sound samples used in this chapter were all recorded at 11KHz. This means that we have thrown away the entire portion of every sample greater than 5.5KHz in frequency. We are also using only eight-bit samples, so we are introducing a significant amount of distortion in the form quantization error.
All these factors are taken into account when designing the hardware and software for digitization. Instead of trying to perfectly reproduce analog phenomena, we instead make compromises that give us reproduction that is satisfactory for our purposes.
Likewise, when we look at lossy compression, we once again accept a certain loss in fidelity. The signal we get after going through a compression/expansion cycle will not be identical to the original, but we can adjust the parameters to get better or worse fidelity, and likewise better or worse compression.
| Previous | Table of Contents | Next |