A Standard That Works: JPEG

In the late 1970s and early 1980s, research began on new types of image compression that promised to greatly outperform the more conventional compression techniques discussed earlier. By the late 1980s, this work was beginning to find commercial applications for image processing on desktop systems, mostly in the form of add-on coprocessor cards for UNIX and Macintosh workstations. These cards were able to perform lossy compression on images at ratios of as much as 95 percent without visible degradation of the image quality.

Other forces at this time combined to start development of an international standard that would encompass these new varieties of compression. There are clear advantages to all parties if standards allowed for easy interchange of graphical formats. The main concern regarding early standardization is the possibility that it would constrain further innovation. The two standardization groups involved, the CCITT and the ISO, worked actively to get input from both industry and academic groups concerned with image compression, and they seem to have avoided the potentially negative consequences of their actions.

The standards group created by these two organizations is the Joint Photographic Experts Group (JPEG). The JPEG standard was developed over the curse of several years, and is now firmly entrenched as the leading format for lossy graphics compression.

The JPEG specification consists of several parts, including a specification for both lossless and lossy encoding. The lossless compression uses the predictive/adaptive model described earlier in this chapter, with a Huffman code output stage, which produces good compression of images without the loss of any resolution.

The most interesting part of the JPEG specification is its work on a lossy compression technique. The rest of this chapter discusses the basics of this technique, with sample code to illustrate its components.

JPEG Compression

The JPEG lossy compression algorithm operates in three successive stages, shown in Figure 11.3.

Figure 11.3  JPEG lossy compression.

These three steps combine to form a powerful compressor, capable of compressing continuous tone images to less than 10 percent of their original size, while losing little, if any, of their original fidelity.

The Discrete Cosine Transform

The key to the compression process discussed here is a mathematical transformation known as the Discrete Cosine Transform (DCT). The DCT is in a class of mathematical operations that includes the well-known Fast Fourier Transform (FFT), as well as many others. The basic operation performed by these transforms is to take a signal and transform it from one type of representation to another.

This transformation is done frequently when analyzing digital audio samples using the FFT. When we collect a set of sample points from an incoming audio signal, we end up with the representation of a signal in the time domain. That is, we have a collection of points that show what the voltage level was for the input signal at each point in time. The FFT transforms the set of sample points into a set of frequency values that describes exactly the same signal.

Figure 11.4 shows the classic time domain representation of an analog signal. This particular signal is composed of three different sine waves added together to form a single, slightly more complicated waveform. Each of the sample points represents the relative voltage or amplitude of the signal at a specific point in time.

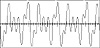
Figure 11.4  The classic time domain representation of an analog signal.

Figure 11.5 shows what happens to the same set of data points after FFT processing. In the time-domain representation of the signal, each of the points on the X axis represents a different point in time, and each of the points on the Y axis represents a specific magnitude of the signal. After processing the data points with an FFT, the X axis no longer has the same meaning. Now, each point on the X axis represents a specific frequency, and the Y axis represents the magnitude of that frequency.

Figure 11.5  Data points after FFT processing.

Given that interpretation of the output of the FFT, Figure 11.5 makes immediate sense. It says that the signal displayed in the earlier figure can also be represented as the sum of three different frequencies of what appears to be identical magnitude. Given this information, it should be just as easy to construct the signal as it would be with Figure 11.4.

Another important point to make about the this type of transformation function is that the function is reversible. In principle, the same set of points shown in Figure 11.5 can be processed through an inverse FFT function, and the points shown in Figure 11.4 should result. The two transformation cycles are essentially lossless, except for loss of precision resulting from rounding and truncation errors.

The DCT is closely related to the Fourier Transform, and produces a similar result. It takes a set of points from the spatial domain and transforms them into an identical representation in the frequency domain; however, we are going to introduce an additional complication in this particular instance. Instead of a two-dimensional signal plotted on an X and Y axis, the DCT will operate on a three-dimensional signal plotted on an X, Y, and Z axis.

In this case, the “signal” is a graphical image. The X and Y axes are the two dimensions of the screen. The amplitude of the “signal” in this case is simply the value of a pixel at a particular point on the screen. For the examples used in this chapter, that is an eight-bit value used to represent a grey-scale value. So a graphical image displayed on the screen can be thought of as a complex three-dimensional signal, with the value on the Z axis denoted by the color on the screen at a given point. This is the spatial representation of the signal.

The DCT can be used to convert spatial information into “frequency” or “spectral” information, with the X and Y axes representing frequencies of the signal in two different dimensions. And like the FFT, there is an Inverse DCT (IDCT) function that can convert the spectral representation of the signal back to a spatial one.