Chapter 4
A Significant Improvement: Adaptive Huffman Coding

In Chapter 3, we saw how Huffman coding could perform effective data compression by reducing the amount of redundancy in the coding of symbols. Huffman coding does not in itself tell how to reduce the information content of each symbol by developing an accurate model. But any model that can calculate the probability of a symbol with any accuracy should be able to use Huffman coding to compress data.

The examples in Chapter 3 all used order 0 models, which are essentially context free. This means that the probability of a given character is calculated without taking into account the characters that preceded it in a message. The programs used in Chapter 3 just analyzed the entire input file and created a table of probabilities for each symbol. As long as these probabilities deviated from a purely uniform distribution, we were able to compress the data.

A minor drawback to Huffman coding programs is the requirement that they transmit a copy of the probability table with the compressed data. The expansion program would have no way of correctly decoding the data without the probability table. The table requires at most the addition of an extra 250 or so bytes to the output table, and consequently it usually doesn’t make much difference in the compression ratio. Even small files won’t be greatly affected, since the probability table should also be small for these files.

The problem with this “minor drawback” is that as we attempt to improve the compression ability of our program, the penalty becomes more and more significant. If we move from order-0 to order-1 modeling, for example, we now have to transmit 257 probability tables instead of just one. So by using a technique that enables us to predict characters more accurately, we incur a penalty in terms of added overhead. Unless the files we are going to compress are very large, this added penalty will frequently wipe out any improvements made by increasing the order.

Adaptive Coding

This seems to lead to an impasse. To compress better, we need to accumulate more statistics. When we get more statistics, we achieve better compression but we wipe out any gains by having to send more modeling data.

Fortunately, there is a way out of this dilemma. Adaptive coding lets us use higher-order modeling without paying any penalty for added statistics. It does this by adjusting the Huffman tree on the fly, based on data previously seen and having no knowledge about future statistics.

Adaptive coding is not something that can just be used with Huffman coding. In principle, almost any form of coding can be converted to use an adaptive method. The high-level C program required to do adaptive compression is shown below.

initialize_model();
do {
     c = getc( input );
     encode( c, output );
     update_model( c );
} while ( c !=  EOF );

The decompressor works in a nearly identical fashion, as shown here:

initialize_model();
while ( ( c = decode( input ) ) ! = EOF ) {
    putc( c, output );
    update_model( c );
}

Adaptive coding works since two of the routines used in these two algorithms are identical: initialize_model() and update_model(). If these routines differed even slightly between the compression and decompression programs, the whole system would fall apart.

This sort of coding is fairly simple. The compressor and decompressor start off with identical models to encode and decode. So when the compressor puts out its very first encoded symbol, the decompressor will be able to interpret it.

After the compressor emits the first symbol, it proceeds to the update_model() function. This is where the adaptive nature of the program begins. The update model takes into account the character that has just been seen and updates the frequency and encoding data used to encode that character. In a Huffman tree, it means incrementing the count for the particular symbol, then updating the Huffman coding tree.

Updating the Huffman Tree

The algorithm for constructing a Huffman coding tree is fairly simple, but it is not something we would want to do after every character is encoded. It would be relatively simple to implement adaptive Huffman coding with the following update function:

update_model( int c )
{
    counts[ c ]++;
    construct_tree( counts );
}

Unfortunately, what we would end up with would probably be the world’s slowest data-compression program. Building the tree takes too much work to reasonably expect to do it after every character.

Fortunately, there is a way to take an existing Huffman coding tree and modify it to account for a new character. All it takes is a slightly different approach to building the tree in the first place. This approach introduces a concept known as the sibling property. A Huffman tree is simply a binary tree that has a weight assigned to every node, whether an internal node or a leaf node. Each node (except for the root) has a sibling, the other node that shares the same parent. The tree exhibits the sibling property if the nodes can be listed in order of increasing weight and if every node appears adjacent to its sibling in the list.

A binary tree is a Huffman tree if and only if it obeys the sibling property. Figure 4.1 shows a Huffman tree that illustrates how this works. In this tree, the nodes have been assigned numbers, with the numbers assigned from left to right starting at the lowest row of nodes and working up. This tree was created using a conventional Huffman algorithm given the weights A=1, B=2, C=2, D=2, and E=10.

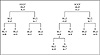
Figure 4.1  A Huffman tree.

In Figure 4.1, the A, B, C, and D nodes at the bottom of the tree are numbered in increasing order starting at 1. Nodes 5 and 6 are the first two internal nodes, with weights of 3 and 4. The node numbers work their way up to node 9, the root. This arrangement shows that this tree obeys the sibling property. The nodes have been numbered in order of increasing weight, and each node is adjacent to its sibling in the list.

The sibling property is important in adaptive Huffman coding since it helps show what we need to do to a Huffman tree when it is time to update the counts. Maintaining the sibling property during the update assures that we have a Huffman tree before and after the counts are adjusted.