| Previous | Table of Contents | Next |
Updating the tree consists of two basic types of operations. The first, incrementing the count, is easy to follow conceptually. To increment the count for symbol ‘c,’ start at the leaf node for the symbol and increment the count for the leaf node. Then move up to the parent node. Since the weight of the parent node is the sum of the weight of its children, incrementing its weight by one will adjust it to its correct value. This process continues all the way up the tree till we reach the root node.
Figure 4.2 shows how the increment operation affects the tree. Starting at the leaf, the increment works its way up the tree till it reaches the parent node. Implementing this portion of the code is relatively simple. Be sure that each node has a parent pointer and that an index points to the leaf node for each symbol. This can be done using conventional data structures at a low cost. The average number of increment operations required will correspond to the average number of bits needed to encode a symbol.

Figure 4.2 The increment process.
The second operation required in the update procedure arises when the node increment causes a violation of the sibling property. This occurs when the node being incremented has the same weight as the next highest node in the list. If the increment were to proceed as normal, we would no longer have a Huffman tree.
When we have an increment that violates the sibling property, we need to move the affected node to a higher point in the list. This means that the node is detached from its present position in the tree and swapped with a node farther up the list.
Figure 4.3 shows the same Huffman tree from Figure 4.2 after the A node has been incremented again, then switched with the D node. How was the D node selected as the one to be switched? To minimize the amount of work during the shuffle, we want to swap just two nodes. If the newly incremented node has a weight of W + 1, the next higher node will have a weight of W. There may be more nodes after the next higher one that have a value of W as well. The swap procedure moves up the node list till it finds the last node with a weight of W. That node is swapped with the node with weight W + 1. The new node list will then have a string of 1 or more weight W nodes, followed by the newly incremented node with weight W + 1.
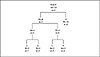
Figure 4.3 After a node switch (only the A node has been incremented).
In Figure 4.3, the A node was incremented from a weight of 2 to 3. Since the next node in the list, the B node, had a weight of 2, the tree no longer obeyed the sibling property. This meant it was time to swap. We worked our way up the list of nodes till we found the last node with a weight of 2, the D node. The A and D nodes were then swapped, yielding a correctly ordered tree.
After the swap is completed, the update can continue. The next node to be incremented will be the new parent of the incremented node. In Figure 4.3, this would be internal node #6. As each node is incremented, a check is performed for correct ordering. A swap is performed if necessary.
What Swapping Does
The swap shown in Figure 4.3 doesn’t have a noticeable effect on the coding of the symbols. The A and D nodes were swapped, but the length of their codes did not change. They were both three bits long before the swap and three bits long after.
Figure 4.4 shows what happens to the three after the A symbol has been incremented two more times. After the second increment, the A node has increased enough to swap positions with an internal node on a higher level of the tree. This reshapes the tree, impacting the length of the codes. When A had a count of two like three other symbols, it was encoded using three bits. Now, when its count has increased to five, it is encoded using only 2 bits. Symbols C is still encoded using 3 bits, but B and D have slipped down to 4 bits.
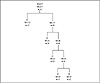
Figure 4.4 After another node switch.
The Algorithm
In summary, the algorithm for incrementing the count of a node goes something like what’s shown below:
for ( ; ; ) {
increment nodes[ node ].count;
if ( node == ROOT )
break;
if ( nodes[ node ].count > nodes[ node + 1 ].count )
swap_nodes();
node = nodes[ node ].parent;
}
The swap_nodes() routine has to move up through the list of nodes until it finds the right node to swap with. It then performs the swap. This routine looks something like that shown below:
swap_node = node + 1;
while ( nodes[ swap_node + 1 ].count < nodes[ node ].count )
swap_node++;
temp = nodes[ swap_node ].parent;
nodes[ swap_node ].parent = nodes[ node ].parent;
nodes[ node ].parent = temp;
An Enhancement
One way to make coding more efficient is to make sure your coder doesn’t waste coding space for symbols not used in the message. With the standard Huffman coding in the previous chapter, this was easy. Since we made a pass over the data to collect statistics before building the tree, we knew in advance which symbols weren’t used. So when we built the Huffman tree we didn’t have to include symbols with a count of 0.
With an adaptive process, we don’t know in advance which symbols will show up in the message. The simplest way to handle this problem is to initialize the Huffman tree to have all 256 possible bytes (for conventional 8-bit data messages) predefined with a count of 1. When the encoding first starts, each message will have a length of eight bits. As statistics accumulate, frequently seen characters will start to use fewer and fewer bits.
This method of encoding works, but in many cases it wastes coding capacity. Particularly in shorter messages, the extra unused codes tend to blunt the effect of compression by skewing the statistics of the message.
A better way to handle this aspect of coding is to start the encoding process with an empty table and add symbols only as they are seen in the incoming message. But this presents us with a seeming contradiction. The first time a symbol appears, it can’t be encoded since it doesn’t appear in the table. So how do we get around this problem?
| Previous | Table of Contents | Next |