| Previous | Table of Contents | Next |
The Escape Code
The answer to this puzzle is the escape code. The escape code is a special symbol sent out of the encoder to signify that we are going to `escape’ from the current context. The decoder know that the next symbol will be encoded in a different context. We can use this mechanism to encode symbols that don’t appear in the currently defined Huffman tree.
In the example program in this chapter, the escape code signifies that the next symbol to be encoded will be sent as a plain 8-bit character. The symbol is added to the table, and regular encoding resumes. The C code to implement the encoder for this algorithm looks something like this:
encode( char c )
{
if ( in_tree( c ) )
transmit_huffman_code( c, out_file );
else {
transmit_huffman_code( ESCAPE, out_file );
putc( c, out_file );
add_code_to_tree( c );
}
update_tree( c );
}
This example shows that the escape code is transmitted like any other symbol from the Huffman tree, so it has to appear in the Huffman tree to be properly transmitted. When the encoder first starts up, it needs to be initialized with the escape code already present.
In the implementation used in the example code for this chapter, the Huffman tree is actually initialized with two values: the escape code and the end of file code. Since both will appear in the file, we start off with them in a very small Huffman tree:
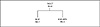
Figure 4.5 A Huffman tree initialized with two values.
As the encoding process goes on, the table fills up and the tree fleshes out. The end of file code will always have a weight of one, and in this implementation, so will the escape code. As the tree grows, these two codes will always be stuck down at the remotest branches of the tree and have the longest codes.
The Overflow Problem
As the compression program progresses, the counts in the table increase. At some point, the counts become large enough to cause trouble for the program. There are two possible areas of concern. The first occurs when the weight of the root exceeds the capacity of the counters in the tree. For most of the programs used here, that will be 16 bits.
Another possible problem can occur even sooner. It happens when the length of the longest possible Huffman code exceeds the range of the integer used to transmit it. The decoding process doesn’t care how long a code is, since it works its way down through the tree a bit at a time. The transmitter has a different problem though. It has to start at the leaf node of the tree and work up towards the root. It accumulates bits to be transmitted in reverse order, so it has to stack them up. This is conventionally done in an integer variable, so this means that when a Huffman code exceeds the size of that integer, there is a problem.
The maximum length of a Huffman code is related to the maximum count via a Fibonacci sequence. A Fibonacci function is defined as follows:
int fib( int n )
{
if ( n <= 1 )
return( 1 );
else
return( fib( n - 1 ) + fib( n -2 ) );
}
The sequence of Fibonacci numbers looks something like this: 1, 1, 2, 3, 5, 8, 13, 21, 34, etc. These numbers show up in the worst-case, most lopsided Huffman tree:
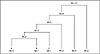
Figure 4.6 A lopsided Huffman tree produced through a sequence of Fibonacci numbers.
From this we can deduce that if the weight at the root node of a Huffman tree equals fib(i), then the longest code for that tree is i - 1. This means that if the integers used with our Huffman codes are only 16 bits long, a root value of 4181 could potentially introduce an overflow. (This low value is frequently overlooked in simple Huffman implementations. Setting up a file with Fibonacci counts up to fib[18] is a good way to test a Huffman program). When we update the tree, we ought to check for a maximum value. Once we reach that value, we need to rescale all the counts, typically dividing them by a fixed factor, often two.
One problem with dividing all the counts by two is that it can possibly reshape the tree. Since we are dealing with integers, dividing by two truncates the fractional part of the result, which can lead to imbalances. Consider the Huffman tree shown in Figure 4.7.
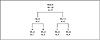
Figure 4.7 A Huffman tree created for four symbols.
This is a tree created for four symbols: A, B, C, and D, with weights of 3, 3, 6, and 6. The nodes of the tree are numbered in this diagram, and the diagram clearly shows that the tree is a Huffman tree, since it obeys the sibling property. The problem with this tree occurs if we try a rescaling operation. The simple version of the rescaling algorithm would go through the tree, dividing every leaf node weight by two, then rebuilding upwards from the leaf nodes. The resulting tree would look like what follows.
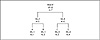
Figure 4.8 The rescaling problem after the nodes are divided by two.
The problem with the resulting tree is that it is no longer a Huffman tree. Because of the vagaries of truncation that follow integer division, we need to end up with a tree that has a slightly different shape:
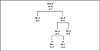
Figure 4.9 What the tree should look like after integer division.
The properly organized Huffman tree has a drastically different shape from what it had before being rescaled. This happens because rescaling loses some of the precision in our statistical base, introducing errors sometimes reflected in the rescaled tree. As time goes on, we accumulate more statistics, and the effect of the errors gradually fades away.
Unfortunately, there is no simple way to compensate for the necessary reshaping the tree after rescaling. The sample code in this chapter merely does a brute-force rebuilding after rescaling. Rebuilding the entire tree is a relatively expensive operation, but since the rescaling operation is rare, we can live with the cost.
| Previous | Table of Contents | Next |