Image compression with Iterated Function Systems

An IFS provides a good approximation of a target image I if the fixed point of the IFS is an image closely resembling I. The goal is to find a set of contractive mappings w₁ ... w_N so that the union W of all these mappings has a fixed point close to I.

It is hopeless to find W by trying some mappings w_j, computing the resulting fixed point, comparing it with I, and starting again with other mappings until a close match is found. We will instead try to find a contractive mapping W such that W(I) is close to I. Barnsley’s Collage Theorem states that if W(I) is sufficiently close to I, then the fixed point

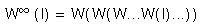
is also close to I. The image W(I) is composed of a collage (union) of all the reduced images w_j (I). This is how the theorem got its name.

So with the help of the Collage Theorem, the “inverse problem” can be restated as finding a good collage for an image. This is where the real difficulties start. It is generally not feasible, even with enormous computing power, to find a good collage automatically, thus human intervention is required. A person must guide the compression process by segmenting the original image so that each segment looks like a reduced copy of the whole image, and so that the union of all segments covers the original image as best as possible. For example, the person determines that a branch of a tree can be viewed as a reduced copy of the whole tree, possibly distorted.

Once the segments have been defined, the computer can derive the w_j mappings and thus an IFS for the image. There is a lot of flexibility in the choice of the mappings, as long as they are contractive, but affine functions are generally used for simplicity. In one dimension, an affine function has the form

f(x) = a * x  +  b

where a and b are constants. In two dimensions, the image of a point X = (x, y) is

f(X) =  A * X + B

where A is a two-dimensional matrix and B a constant vector. The matrix A determines a rotation, skew and scaling for the image, and the vector B determines a translation. The contractivity condition on f can be expressed as conditions on the coefficients of the matrix A: the scaling factor must be less than one.

After all the affine transformations have been selected, the IFS can be represented in a compact form by encoding the coefficients of all the transformations. If a good collage has been found, the total number of affine transformations is much smaller than the total number of pixels in the image, so encoding the coefficients requires far fewer bits than enumerating all the pixel values. This is why encoding an image as an IFS is actually a form of data compression. The compression is lossy because the attractor of the IFS is in the best case close to the original image but not strictly equal to it.

The main difficulty of this compression process is to find within the image reduced copies of the whole image. Real-world images often contain some self-similarity, but only between selected portions of the image. The breakthrough made by Jacquin was to partition the input image, and to find a local IFS for each partition. With this new method, it finally became possible to completely automate the compression process and furthermore to do it in a reasonable amount of time.

Image compression with Partitioned Iterated Function Systems

We have seen in chapter 8 “Sliding Window Compression” that the LZ77 algorithm works by finding redundancy within the input text in the form of common phrases. Similarly, some image compression algorithms such as Vector Quantization and Fractal compression with PIFS work by finding redundancy within the input image in the form of similar image portions. The parallel between the text and image compression methods is not complete since the former are lossless, whereas the latter only look for approximate matching and are thus lossy.

Vector Quantization uses a dictionary (or codebook) of pixel patterns. The input image is partitioned into small pixel blocks, and each block is encoded as a reference to the dictionary pattern which most resembles the block. A block has the same size as the corresponding dictionary pattern, but all the blocks need not have the same size. The decoder must have a copy of the dictionary, and can easily reconstruct an approximation of the original image by assembling the dictionary patterns specified by the encoder.

Fractal compression with PIFS is similar to Vector Quantization, but in this case, there is no external dictionary. The input image acts as its own dictionary. The decoder doesn’t have this image initially, but it can reconstruct it gradually by iterating a PIFS. Thus the dictionary is only a “virtual codebook”.