The compressor first partitions the input image into a set of non-overlapping ranges. The ranges are generally squares or rectangles, but good results can also be obtained with other shapes such as triangles. For each range, the compressor looks for a part of the input image called a domain, which is similar to the range. The domain plays the role of the pixel pattern in Vector Quantization, but here it must be larger than the range to ensure that the mapping from the domain to the range is contractive in the spatial dimensions.

---

Note:  Barnsley has reversed the meanings of range and domain, but we prefer keeping the established terminology: a transformation maps from a domain to a range.

---

In general, the compressor looks for domains that are twice as large as the range, but other ratios are possible. As opposed to ranges, domains may overlap.

The test file LISAW.GS is shown in Figure 13.1. The same file compressed with fractal compression at a compression ratio of 96% is shown in Figure 13.2.

Figure 13.1  The original LISAW.GS (64000 bytes).

Figure 13.2  LISAW with fractal compression (2849 bytes).

In Figure 13.2, two ranges and the two corresponding domains selected by the compression algorithm have been highlighted. The algorithm has found similarity between two unrelated portions of the image: a range below the eye and a domain, twice as large, on the forehead. The compressor has also found self-similarity within one domain, in the chin. In the latter case, the range and the domain overlap. This kind of self-similarity is quite frequent in real-world images, and fractal compression takes advantage of this.

To assess the similarity between a domain D and a range R, the compressor finds the best possible mapping w from the domain to the range, so that the image w(D) is as close as possible to the image R. As we have seen previously, affine transformations are convenient for this purpose, but non-linear transformations could also be used as long as they are contractive. Two-dimensional transformations were used for black and white images. Three dimensions are needed for grey scale images: two for the spatial components and one for the luminance component. An affine map is then composed of a geometric part which maps the domain into the range, and of a luminance part which changes the pixel intensity values.

More precisely, a point (x, y) with luminance z belonging to domain D_i is mapped into:

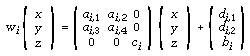
The constants a_i,j and d_i,j specify the geometric part, the constants c_i and b_i specify the luminance part. c_i represents a contrast factor, which must be smaller than one to make sure that the mapping is contractive in the luminance dimension. b_i represents a brightness offset applied after the contrast has been reduced.

In practice, the compressor does not have to determine explicitly the constants a_i,j and d_i,j for each domain. They are implicitly defined by the relative size, orientation and position of the domain with respect to the range. In particular, if the compressor only looks for domains that are exactly twice as large as the range, the scaling factor which would normally be derived from the a_i,j values is already imposed and is equal to 0.5. Similarly, if domains and ranges are restricted to be squares, there are only 8 possible orientations of the domain relative to the square: 4 rotations and 4 symmetries. Thus 3 bits are sufficient to encode this orientation. Finally, the translation constants d_i,j are determined by the position of the top left corner of the domain.

The simplifications described above may seem too drastic, but they are actually necessary to reduce the complexity of the “inverse problem” to manageable proportions. In theory, ranges and domains can have potato shapes instead of a square shape, the contractive mappings can be non linear instead of being affine maps, etc... However the total search space would become much too large and as a result the compression would be too slow for practical use. But even with simple affine maps, finding the optimal domain for a given range can still be an expensive operation.

For a given range R, the compressor must examine a number of possible domains. For each such domain D, the compressor must find the optimal affine map from D to R. The best one is the map w which minimizes the distance between the image R and the image w(D), where the distance is taken in the luminance dimension, not the spatial dimensions.

Such a distance can be defined in various ways, but to simplify the computations it is convenient to use the Root Mean Square (RMS) metric (the program GSDIFF.C given in the previous chapter computes such a distance). For a given range and and a given domain, the RMS distance depends only on the contrast factor c_i and the brightness offset b_i The distance is minimum when the partial derivatives with respect to these two variables are both zero. c_i and b_i can thus be obtained by solving two simple linear equations, as we will see later in our sample fractal compression program.

Once the RMS distances between the range and all selected domains have been determined, the compressor chooses the domain with the smallest distance, encodes the corresponding affine map, and goes on working on the next range.